Origin Story: The Quad

February 14, 2022

It started as a casual meet-up at a downtown Berkeley cafe. Professor Dor Abrahamson planned to do a little humble bragging with his latest tablet app, the Mathematics Imagery Trainer, designed for middle schoolers to learn ratio and proportions, which he'd rigged up to include beeping noises for sight-impaired students.

Within minutes of his conversation with Engineering PhD Josh, it was Professor Abrahamson who was humbled.

In that 30-minute exchange, Professor Abrahamson's 20+ years of educational theory flashed before his very eyes. And then he found an opportunity.

Read below as Professor Abrahamson recounts the intriguing origin story of The Quad, a hand-held, versatile quadrilateral that, when blue-toothed to a computer, allows sighted and sight-impaired students to learn geometry -- together.

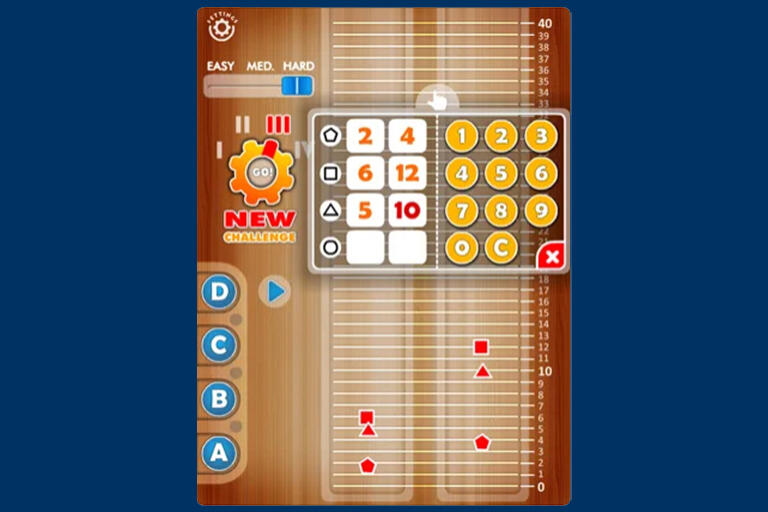
I was both mortified and inspired, one Tuesday, back in September, 2017, when Josh and I met for coffee at Au Coquelet Café on the corner of Milvia St. and University Avenue. Josh is an engineer, a Berkeley PhD in psychoacoustics, and an inventor of technological solutions for blind professionals to manage complex quantitative data sets. I was presenting to Josh a tablet app I had designed for kids to learn the math concept of ratio and proportions, such as 2:3 = 4:6. In this app, you slide your two index fingers, the left and the right, up along the interface at different speeds. If you move them at the correct speeds relative to each other, so that they are always 2 and 3 units above the bottom line, respectively, the screen will be green.

But green doesn’t mean too much for Josh, who is blind, and so I proudly switched on the alternative sound feedback, a semi-pleasant beep. I watched Josh work. Indeed, he slid his fingers up the screen, seeking the beep. But he also did something else that I had not seen anyone do before, and this after ten years of developing this activity, using mechanical pullies, Wii-mote, Kinect, and LeapMotion remote sensors, mouse, trackpad and, now, tablet: Josh used his thumbs, too: he looped each thumb around the tablet’s exterior encasing, even as he slid the index up. Now why would he do that?

“Why are you using your thumbs, Josh?” It was truly mysterious to me. It appeared contrived, contorted, and darn right confusing. “Well,” he retorted, a tad bemused, “If I don’t keep my thumbs down there as I move my indexes up here, how will I know where I am? How would I gauge the ratio of these two gaps? I’m blind, Dor. Hello?” I was mortified.

Mortified, because Josh was stating the obvious. “You, sighted people,” Josh went on, “You go on and on about visual this and visual that. But vision is not the thing itself, it’s just a way of getting at the thing itself—what counts is space, the spatial arrangements of stuff in the world. I can’t see, but I know what things are and where things are. I feel, I hear, I can get from place to place. Vision is just one conduit for the real thing, which is actually the size and place of things. It’s about spatial relations, like in this app.” And the app beeped, a nice continuous semi-pleasant triumphant beep. Fifteen–love.

Play slideshow
Mathematics Imagery Trainer
Play video
The Quad, a hand-held geometric manipulative for sighted and sight-impaired students to learn mathematics -- together.

More than just a beep

Yet inspired, too, I was, because it then hit me—smashed me—for the very first time, and truly, deeply, madly, at that, that I’m a bigoted sightist. The more genteel descriptor of my prejudice, I would find out later, would be ocularcentrist. And here I was, designing my meager beep for blind and visually impaired mathematics students, a sorry substitute indeed. What did I know?

Still, though, inspired, because I had just received the best lesson ever on sensation and perception since that Cognitive Psychology 101 undergraduate course I took in the Fall of 1992. Inspired, because a new world had just opened to my mind, one beyond eyes and into hands, into sensory modalities such as the shape of things in our palm, the rich range of frictive surfaces on our fingertips, the multifarious experiences of moving, reaching, grasping, hearing, rocking, jumping. All these ways of making sense, all these perfectly competent ways of learning. No eyes, yet a full dexterous booming buzzing life. A life I had not seen. “Josh,” I said, inveterate academician that I am, “there’s a paper here.”

And a year later, there was a paper here, and yet a year after that, it was out. A conceptual paper, it was, where we argued that the field should rethink the teaching and learning of mathematics for differently abled people. Because, clearly, replacing green with a beep won’t cut it. That had been just me and my ignorance, believing that one should build for typical folks but then patch it up, post facto, for other folks, embedding into a finessed gizmo some topical salve that would do the trick for the other guys. But it doesn’t do the trick. It doesn’t do the trick, because such a process of designing educational technologies assumes there is only a superficial difference between people with different sensory experiences, as though we know the world essentially the same. This assumption is implicit—the designers’ insidious assumption, harbored by those who cannot see how differently we experience the world.

Sensory, mobility, and cognitive diversity

But, others have also recognized experiences of modal diversity as opportunities for advancing knowledge, inclusion, and social justice. For, one thing led to another, and that paper, once out in 2019, attracted interest from my collaborator-to-be Emily, from the University of Colorado, Boulder. She herself had been inspired by a young blind woman’s reflection of middle school exclusion while classmates experienced the now classic Oregon Trail computer learning game. A leader in the world-renown PhET Interactive Simulations project, Emily had spent the last six years advancing research, design, and technical infrastructure. Her goal—to ensure that no child is excluded from the shared joy and learning that simulations engender in science and mathematics classrooms, regardless of sensory, mobility, or cognitive diversity. Initially motivated to bring into the world accessible ‘layers’ to the PhET simulations (e.g., adding sound and description options to the visuals), Emily has since come to recognize that a paradigm shift in technology-enhanced learning is needed if we are to create truly egalitarian inclusive classrooms. Even the most sophisticated beeps and descriptions will struggle to result in intuitive and authentic collaboration between sensorially-diverse learners if designs must conform to intrinsically ocularcentrist constraints. 

Emily's knowledge in multimodal design and development, and the involvement of her team of experts in accessibility and design with learners with disabilities, coupled with the capabilities of PhET’s multimodal software infrastructure—all at the bleeding edge of today’s technologies—have allowed us, together, henceforth, to leapfrog directly into the creation of novel multimodal learning tools, and address central questions of cognition and learning. Immediately, though, emerged the perennial philosophical quandaries: Do mathematical concepts exist out there, and we each apprehend them according to our respective modal inclinations, whether as sound, touch, or sight? Lo, no! But yet if we eschew such staunch metaphysical realism, and consider, instead, that mathematical concepts are fictive simulacra, figments of our cultural–historical collective imaginations, where does that leave us?

Is my 2:3 ratio the same as Josh’s? If not, how can we talk about it, as though we agree on its inherent nature? What do we share? In fact, for that matter, what do any two people actually share, when they talk about things of such tenuous palpability as a 2:3 ratio? What do two people come to share, when they learn together? And yet how would Josh and I—fade out, rewind half a century earlier, fade in—study together? Could we? Because clearly Josh thinks differently than I do. And yet in what sense? What might it mean for the two of us to be desk buddies in a 6th grade classroom, coming to know a new mathematical concept together? What instructional methodology could bring that about?—What tools, activities, what norms of discourse? Had I been graced with such a classroom, I would not need fifty years to go by before I was enriched forever by Josh’s sarcastic retort. “I’m blind, Dor, what do you expect?” Imagine.

A convergence of theory, technology, and methods

Fifty years later, and fading back in, these are exciting times to be a scientist of human learning with an interest in mathematics cognition, learning, and teaching, because three major historical efforts in scholarship and engineering are now coming to a head, converging, enabling us to rethink the inclusive classroom, to reimagine universal solutions for diverse cohorts. The three efforts are in theory, technology, and methods.

THEORY

Recent decades have seen substantial efforts across the disciplines of philosophy and cognitive science to rethink fundamental problems of epistemology and ontology. I am referring to a paradigm change from Cartesian to post-Cartesian conceptualizations of the human mind. Read more. ...

We have been captured for half a century in a view of the mind as a computer—with input of sensations, central processing of abstract symbols, and outputs of actions. But now many of us are seriously considering that what we call cognitive activity is not dissociated from the sensorimotor cerebral faculties but, rather, is inherently constituted by sensorimotor operations. These sensorimotor operations are, in turn, embedded in the phenomenal world. Knowledge is not a noun—it is a verb, it is ‘knowing.’

Granted, much of what we learn is held as biological changes in the neural composition of the brain—it is, in a sense, stored as chemical structures. But the activity of thinking is a modal experience that incorporates features of the phenomenal world and may even transform the phenomenal world to support the thinking. Learning is the activity of adapting to the natural and sociocultural environment, replete with fellow human beings and historical practices and artifacts. We internalize structures that we come to perceive in the natural and sociocultural environment, so that thinking, even when you are sitting in your chair with your eyes closed, actuates the brain’s sensorimotor faculties and uses cultural forms. Thinking is imaginary doing. Now, if thinking is an imaginary activation of sensorimotor capacity, then if we want people to think in new ways then we need to create conditions for them to move in new ways.

By this token, strange as it may beep, mathematical concepts are not abstract. They are imaginary. There’s a difference. Mathematical concepts are sensorimotor enactments: To the mind, they are just like actually doing something with stuff. If you cannot imagine enacting a concept, these theories pontificate, you have not understood it—you have not grasped it. When people say that mathematical concepts are abstract, they mean that mathematical ontologies are not material. Granted. Yet, still, the cognitive actions of reasoning a mathematical concept are the same or very similar to what we would do to material ontologies. And that is what counts—the phenomenology, the cognition. For that is the locus, focus, hocus-pocus, nexus, and substance of reasoning, knowing, learning, teaching.

TECHNOLOGY

With existing technologies, it is now possible to develop Embodied Interaction Interfaces, which create working environments that solicit the user’s naturalistic multimodal forms of engagement. They are designed to support the user’s sensorimotor perception and handling of situations involving objects, whether these objects are concrete, virtual, or even imaginary. Read more. ...

In contrast to commercial designers who seek to create user interfaces where embodied interaction is seamless and “invisible”—that is, they aim to minimize or remove any learning curve—educational designers may choose deliberately to create a situation where the user (the student) must struggle to enable the manipulation of a situation according to the tasks’ needs. In a sense, we can design for students to learn a new natural user interface, that is, to make a new form of embodied interaction familiar and, eventually, seamless.

These new patterned forms of embodied interaction could embody dynamical expressions of ideas, such as mathematical concepts.

METHODS

We now have a vast range of instruments to measure and monitor biological markers of physiological and neural activity. If you think of popular commercial products, such as various sports gear for quantifying your cardiovascular activity as you go jogging in your favorite park, then you know what I’m talking about. Read more. ...

This equipment, which turns your body into a moving laboratory, is useful for educational research, too, because it can capture activity and changes in biosensors believed to indicate cognitive efforts to solve problems. That is, we the researchers can monitor the biology and kinesiology of learning, sometimes even as it is happening. Moreover, not only do we capture information from multiple modalities of sensation and action, we can analyze and visualize this information in search of patterns.

For example, we can capture and monitor where a person is attending, using eye-tracking instruments or computer vision in postprocessing, and then compare that information to the quality of another collaborating person’s handling objects in some task, and to the clinical data of what these persons are telling us about their thoughts and experience.

With modern computing power it is now possible to analyze the immense data sets generated from moment-to-moment biosensor tracking, allowing for complementary use of learning analytics and time-honored qualitative approaches to triangulate new insights of human cognition and learning.

Learning is moving in new ways

And so, theory, technology, and methods. Yet, as Venn diagrams always suggest, it is at the intersections that the rhetorical interest lives and thrives. The PhET team seeks to advance the theory, design methods, and technical infrastructure that inform the development of multimodal science and mathematics learning environments, and so find themselves entwined within the challenges and potential of these fields. For me, I locate much of my laboratory’s work at the intersection of these three spheres of scholarship and engineering. At UC Berkeley's Embodied Design Research Laboratory (EDRL), we are evaluating embodiment theory on pedagogical problems, and we are doing so by engaging students in problem-solving activities that are deployed in embodied-interaction interfaces. We capture the students’ problem-solving process by measuring their multimodal sensorimotor activity, and we analyze this activity to understand the micro-process of mathematics learning.

Joining together the complementary expertise of EDRL and PhET, we have been collaborating to expand to populations of diverse sensorial, cognitive, and linguistic access. In so doing, we are advancing the slogan that “Learning is moving in new ways.” One meaning of this slogan is the hypothesis that the cognitive activity of mathematical reasoning draws on sensorimotor perceptions enabling effective interaction in the world. As such, we attempt to create conditions for students to develop new sensorimotor perceptions that, we believe, lend meaning to what become mathematical concepts.

But another meaning of this slogan is that human learning, as a phenomenon of study, is moving in new ways—in the sense that the new cognitive paradigm is transforming scholarship on human learning. So that Josh and I could study ratio together.

Additional Items of Note
  • Professor Abrahamson's 2019 paper appeared in ZDM Mathematics Education. A PDF of the paper can be found here.
  • Abrahamson, D., Flood, V. J., Miele, J. A., & Siu, Y.-T. (2019). Enactivism and ethnomethodological conversation analysis as tools for expanding Universal Design for Learning: The case of visually impaired mathematics students. ZDM Mathematics Education, 51(2), 291-303. https://doi.org/10.1007/s11858-018-0998-1
  • Check out the PhET accessible version of Professor Abrahamson’s Mathematics Imagery Trainer for Proportion.